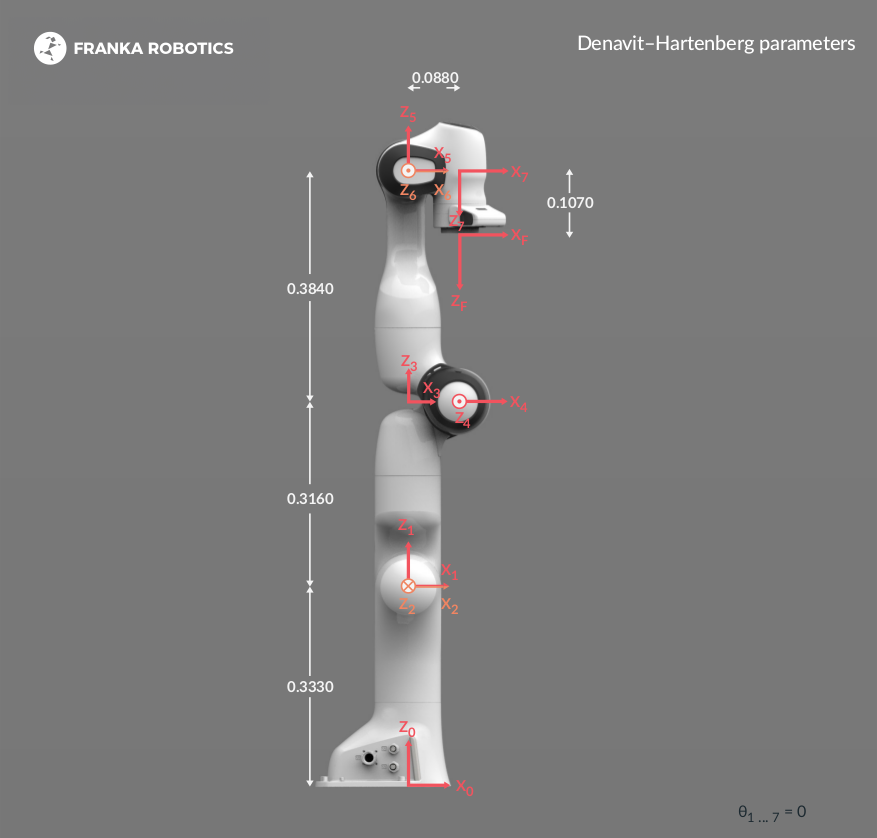
机器人与接口规范¶
发送到机器人的实时控制命令应满足 推荐的 和 必要的 条件。应满足推荐条件以确保机器人的最佳运行。如果不满足必要条件，则运动将中止。
最终的机器人轨迹是对用户指定的轨迹进行处理的结果，以确保满足推荐条件。只要满足必要条件，机器人就会尝试遵循用户提供的轨迹，但只有在最终轨迹也满足推荐条件的情况下，它才会与最终轨迹相匹配。如果违反了必要条件，则错误将中止运动：例如，如果用户定义的关节轨迹的第一点与机器人的起始位置有很大差别 (\(q(t=0) \neq q_c(t=0)\)) ，那 start_pose_invalid 错误将中止运动。
下面公式中使用的常数值在 常数 部分列举。
关节轨迹要求¶
必要条件¶
- \(q_{min} < q_c < q_{max}\)
- \(-\dot{q}_{max} < \dot{q}_c < \dot{q}_{max}\)
- \(-\ddot{q}_{max} < \ddot{q}_c < \ddot{q}_{max}\)
- \(-\dddot{q}_{max} < \dddot{q}_c < \dddot{q}_{max}\)
推荐条件¶
- \(-{\tau_j}_{max} < {\tau_j}_d < {\tau_j}_{max}\)
- \(-\dot{\tau_j}_{max} < \dot{\tau_j}_d < \dot{\tau_j}_{max}\)
在轨迹开始时，应满足以下条件：
- \(q = q_c\)
- \(\dot{q}_{c} = 0\)
- \(\ddot{q}_{c} = 0\)
在轨迹结束时，应满足以下条件：
- \(\dot{q}_{c} = 0\)
- \(\ddot{q}_{c} = 0\)
笛卡尔轨迹要求¶
必要条件¶
- \(T\) 是合适的变换矩阵
- \(-\dot{p}_{max} < \dot{p_c} < \dot{p}_{max}\) (笛卡尔速度)
- \(-\ddot{p}_{max} < \ddot{p_c} < \ddot{p}_{max}\) (笛卡尔加速度)
- \(-\dddot{p}_{max} < \dddot{p_c} < \dddot{p}_{max}\) (笛卡尔加加速度/加速度变化率)
从逆运动学中导出的条件：
- \(q_{min} < q_c < q_{max}\)
- \(-\dot{q}_{max} < \dot{q_c} < \dot{q}_{max}\)
- \(-\ddot{q}_{max} < \ddot{q_c} < \ddot{q}_{max}\)
推荐条件¶
从逆运动学中导出的条件：
- \(-{\tau_j}_{max} < {\tau_j}_d < {\tau_j}_{max}\)
- \(-\dot{\tau_j}_{max} < \dot{{\tau_j}_d} < \dot{\tau_j}_{max}\)
在轨迹开始时，应满足以下条件：
- \({}^OT_{EE} = {{}^OT_{EE}}_c\)
- \(\dot{p}_{c} = 0\) (笛卡尔速度)
- \(\ddot{p}_{c} = 0\) (笛卡尔加速度)
在轨迹结束时，应满足以下条件：
- \(\dot{p}_{c} = 0\) (笛卡尔速度)
- \(\ddot{p}_{c} = 0\) (笛卡尔加速度)
常数¶
笛卡尔空间的限制如下：
| Name | Translation | Rotation | Elbow |
|---|---|---|---|
| \(\dot{p}_{max}\) | 1.7000 \(\frac{\text{m}}{\text{s}}\) | 2.5000 \(\frac{\text{rad}}{\text{s}}\) | 2.1750 \(\frac{rad}{\text{s}}\) |
| \(\ddot{p}_{max}\) | 13.0000 \(\frac{\text{m}}{\text{s}^2}\) | 25.0000 \(\frac{\text{rad}}{\text{s}^2}\) | 10.0000 \(\;\frac{rad}{\text{s}^2}\) |
| \(\dddot{p}_{max}\) | 6500.0000 \(\frac{\text{m}}{\text{s}^3}\) | 12500.0000 \(\frac{\text{rad}}{\text{s}^3}\) | 5000.0000 \(\;\frac{rad}{\text{s}^3}\) |
关节空间限制如下：
| Name | Joint 1 | Joint 2 | Joint 3 | Joint 4 | Joint 5 | Joint 6 | Joint 7 | Unit |
|---|---|---|---|---|---|---|---|---|
| \(q_{max}\) | 2.8973 | 1.7628 | 2.8973 | -0.0698 | 2.8973 | 3.7525 | 2.8973 | \(\text{rad}\) |
| \(q_{min}\) | -2.8973 | -1.7628 | -2.8973 | -3.0718 | -2.8973 | -0.0175 | -2.8973 | \(\text{rad}\) |
| \(\dot{q}_{max}\) | 2.1750 | 2.1750 | 2.1750 | 2.1750 | 2.6100 | 2.6100 | 2.6100 | \(\frac{\text{rad}}{\text{s}}\) |
| \(\ddot{q}_{max}\) | 15 | 7.5 | 10 | 12.5 | 15 | 20 | 20 | \(\frac{\text{rad}}{\text{s}^2}\) |
| \(\dddot{q}_{max}\) | 7500 | 3750 | 5000 | 6250 | 7500 | 10000 | 10000 | \(\frac{\text{rad}}{\text{s}^3}\) |
| \({\tau_j}_{max}\) | 87 | 87 | 87 | 87 | 12 | 12 | 12 | \(\text{Nm}\) |
| \(\dot{\tau_j}_{max}\) | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | \(\frac{\text{Nm}}{\text{s}}\) |
当关节 4 具有角度 \(q_{elbow-flip}\) 时，手臂可以达到其最大伸展，其中 \(q_{elbow-flip} = -0.467002423653011\:rad\)。该参数用于确定肘部的翻转方向。
Denavit–Hartenberg 参数¶
Panda 运动链的DH参数是根据 Craig 约定导出的，如下所示：
Panda的运动链
| Joint | \(a\;(\text{m})\) | \(d\;(\text{m})\) | \(\alpha\;(\text{rad})\) | \(\theta\;(\text{rad})\) |
|---|---|---|---|---|
| Joint 1 | 0 | 0.333 | 0 | \(\theta_1\) |
| Joint 2 | 0 | 0 | \(-\frac{\pi}{2}\) | \(\theta_2\) |
| Joint 3 | 0 | 0.316 | \(\frac{\pi}{2}\) | \(\theta_3\) |
| Joint 4 | 0.0825 | 0 | \(\frac{\pi}{2}\) | \(\theta_4\) |
| Joint 5 | -0.0825 | 0.384 | \(-\frac{\pi}{2}\) | \(\theta_5\) |
| Joint 6 | 0 | 0 | \(\frac{\pi}{2}\) | \(\theta_6\) |
| Joint 7 | 0.088 | 0 | \(\frac{\pi}{2}\) | \(\theta_7\) |
| Flange | 0 | 0.107 | 0 | 0 |
注解
\({}^0T_{1}\) 是描述 坐标系 1 在 坐标系 0 中的位置和方向的变换矩阵。运动链可以如下计算： \({}^0T_{2} = {}^0T_{1} * {}^1T_{2}\)